Interpret histograms
Key Notes:
1. Understanding Histograms
- A histogram is a type of bar graph that represents the distribution of numerical data by showing the frequency of data points within specified intervals (bins).
- Unlike bar graphs, histograms display data that is continuous, meaning the bars touch each other.
2. Parts of a Histogram
- Title: Describes what the histogram represents.
- X-axis (Horizontal axis): Represents the intervals or bins of data, showing the range of values grouped together.
- Y-axis (Vertical axis): Represents the frequency or count of data points within each interval.
- Bars: Each bar represents the frequency of data points within a specific interval. The height of the bar corresponds to how many data points fall within that interval.
3. Steps to Interpret a Histogram
- Step 1: Read the Title: Understand what the histogram is about.
- Step 2: Analyze the X-axis: Look at the intervals to understand the range of data being represented.
- Step 3: Analyze the Y-axis: Check the scale to understand the frequency of data points.
- Step 4: Examine the Bars: The height of each bar indicates how many data points fall within the corresponding interval.
- Step 5: Draw Conclusions: Use the histogram to identify patterns, such as which interval has the most or least data points.
4. Identifying Key Features in Histograms
- Peak (Mode): The tallest bar represents the interval with the highest frequency, also known as the mode.
- Spread: Look at how wide the data is spread across the intervals. This shows the range of the data.
- Skewness:
- Left-skewed (negative skew): Most data points are concentrated on the right side.
- Right-skewed (positive skew): Most data points are concentrated on the left side.
- Symmetrical: Data is evenly distributed on both sides of the peak.
5. Comparing Histograms
- Compare different histograms by looking at the spread, peak, and skewness to understand how the distributions differ.
- Compare the height of bars in different histograms to see which data set has more frequent values within certain intervals.
6. Common Mistakes to Avoid
- Misinterpreting the intervals: Remember that each bar represents the frequency of data within a specific interval, not individual values.
- Confusing histograms with bar graphs: Unlike bar graphs, the bars in histograms touch because the data is continuous.
7. Applications of Histograms
- Histograms are often used in statistics to display the distribution of data points, such as test scores, temperatures, or any other quantitative data.
- They help in identifying the central tendency, spread, and overall shape of the data distribution.
Learn with an example
📡 A biscuit factory monitored the number of broken biscuits per pack yesterday.
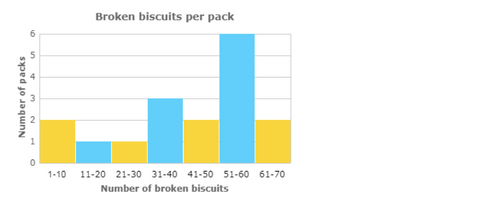
📡 How many packs are there in all?—–packs.
Read the height of each bar off the graph.
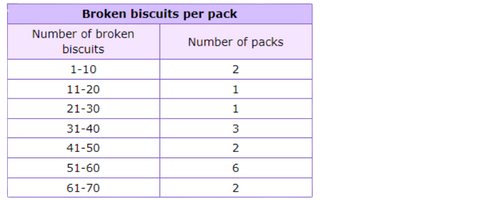
Add to find the total number of packs.
2 + 1 + 1 + 3 + 2 + 6 + 2=17
There are 17 packs in all.
📡 Brody decided to record the temperature every morning when he woke up.
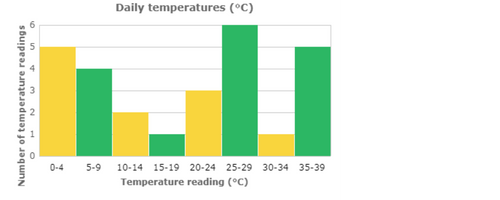
📡 How many temperature readings are there in all?——temperature readings.
Read the height of each bar off the graph.
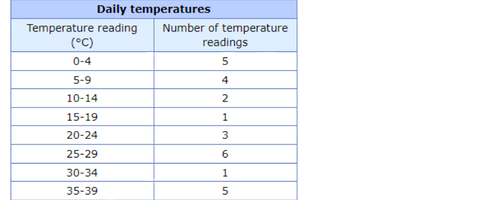
Add to find the total number of temperature readings.
5 + 4 + 2 + 1 + 3 + 6 + 1 + 5=27
There are 27 temperature readings in all.
📡 A farmer counted the number of apples on each tree in her orchard.
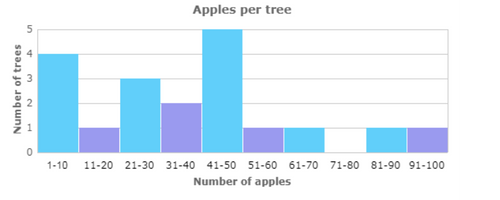
📡 How many trees have between 61 and 70 apples?—–trees.
Find the bar for the range 61-70. Using the scale on the left side of the graph, read the height of the bar. The height of the bar is 1.
1 tree has between 61 and 70 apples.
let’s practice!

