Factorise quadratics using algebra tiles
key notes :
Understanding Algebra Tiles
Algebra tiles are manipulatives that represent algebraic expressions visually.
Different tiles represent different terms:
- Large square: x2
- Rectangle: x
- Small square: Constant (1)
Structure of a Quadratic Expression
- A quadratic expression is in the form ax2 + bx + c
- Factorising means rewriting it as a product of two binomials: (x + m)(x + n).
Arranging Tiles to Form a Rectangle
- Place the x2 tile(s) in one section.
- Arrange x tiles to represent the middle term.
- Place unit tiles for the constant term.
- The goal is to form a complete rectangle.
Finding the Factors
- Identify two numbers that multiply to c and add to b.
- These numbers determine how the tiles are grouped into rows and columns.
Writing the Factored Form
The binomial factors correspond to the dimensions of the rectangle.
Example: If the factors are (x + 3)(x + 2), this means:
- The length of the rectangle = x + 3
- The width of the rectangle = x + 2
Checking the Factorisation
- Expand the binomials to verify:
(x + m)(x + n) = x2 + (m + n) x + mn.
Special Cases
- Perfect square trinomials: Tiles form a square (e.g., x2 + 6x + 9 = (x + 3)(x + 3).
- Difference of squares: No middle term, factors as (x + a)(x − a).
Benefits of Using Algebra Tiles
- Provides a visual and hands-on approach to learning.
- Helps students understand the connection between area and factorisation.
- Makes abstract algebra more concrete and intuitive.
Learn with an example
🥎 Which area model represents the factorisation 6x2+7x+2=(3x+2)(2x+1)?
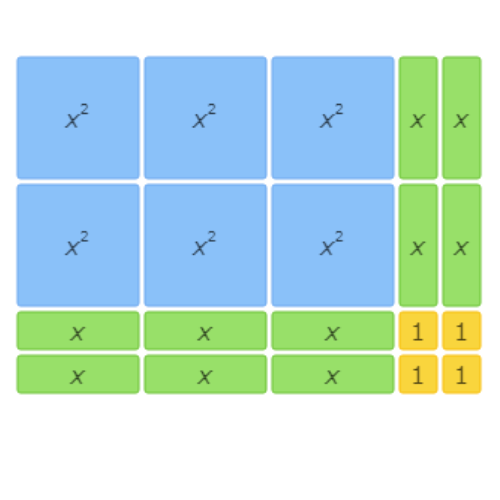
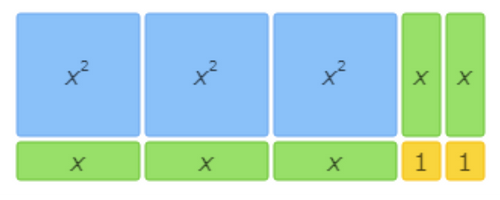
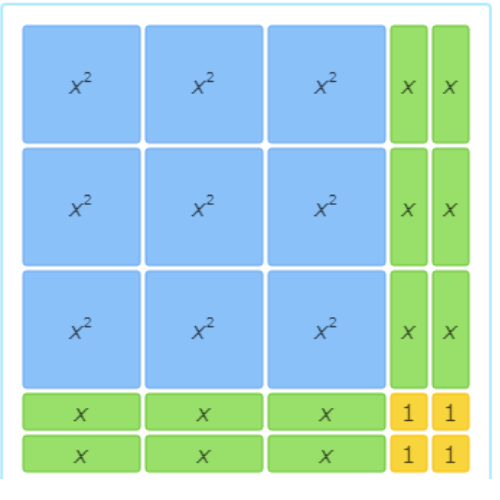
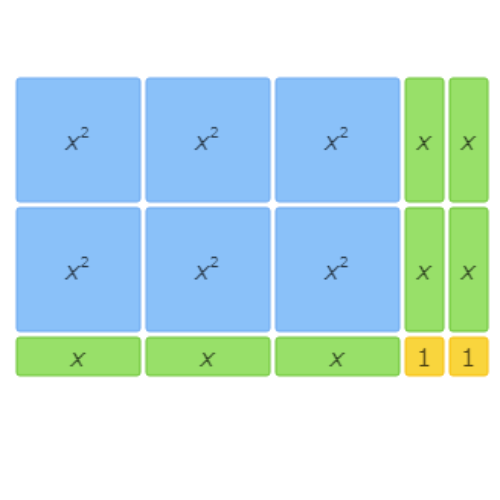
This area model represents the factorisation 6x2+7x+2=(3x+2)(2x+1).
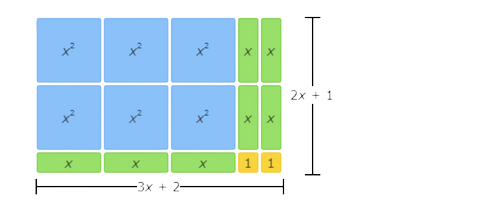
The left side of the equation represents the total area written as the sum of all the tiles. There are 6 x2 tiles, 7 x tiles, and 2 1 tiles, so the sum is 6x2+7x+2.
The right side of the equation represents the total area written as base times height. The base is made up of 3 x tiles and 2 1 tiles, so it is (3x+2). The height is made up of 2 x tiles and 1 1 tile, so it is (2x+1). The base times the height is (3x+2)(2x+1).
The other area models represent factorisations of different polynomials.
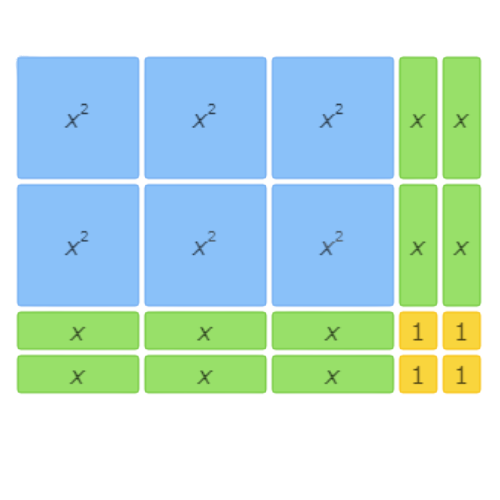
This area model shows 6x2+10x+4=(3x+2)(2x+2).
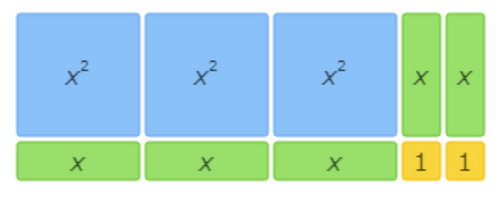
This area model shows 3x2+5x+2=(3x+2)(x+1).
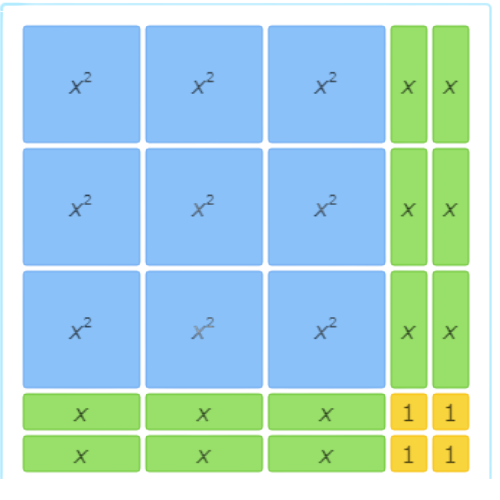
This area model shows 9x2+12x+4=(3x+2)(3x+2).
🥎 Which area model represents the factorisation 4x2+8x+3=(2x+3)(2x+1)?
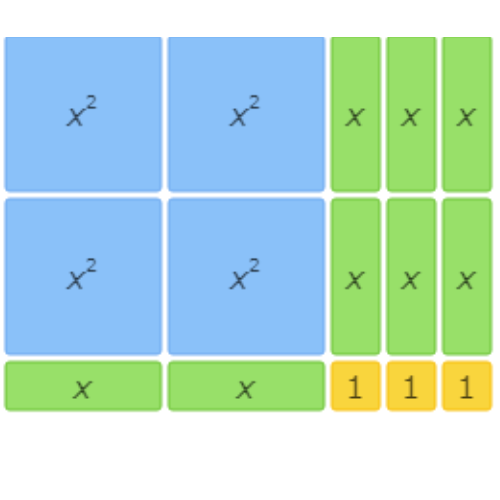
This area model represents the factorisation 4x2+8x+3=(2x+3)(2x+1).
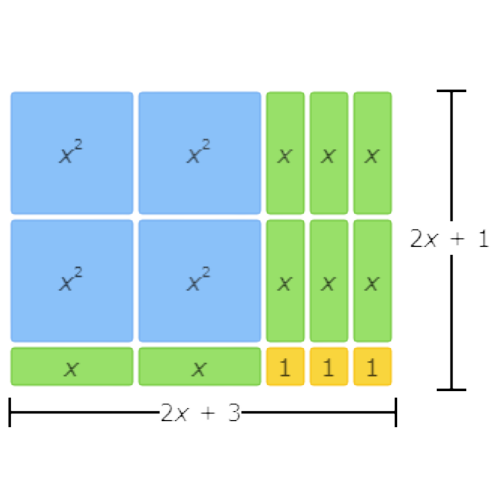
The left side of the equation represents the total area written as the sum of all the tiles. There are 4 x2 tiles, 8 x tiles, and 3 1 tiles, so the sum is 4x2+8x+3.
The right side of the equation represents the total area written as base times height. The base is made up of 2 x tiles and 3 1 tiles, so it is (2x+3). The height is made up of 2 x tiles and 1 1 tile, so it is (2x+1). The base times the height is (2x+3)(2x+1).
The other area models represent factorisations of different polynomials.
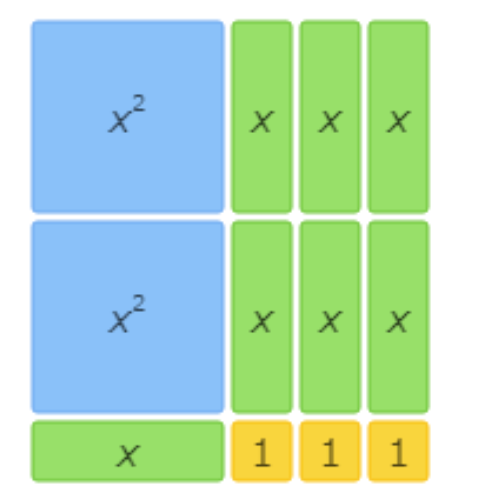
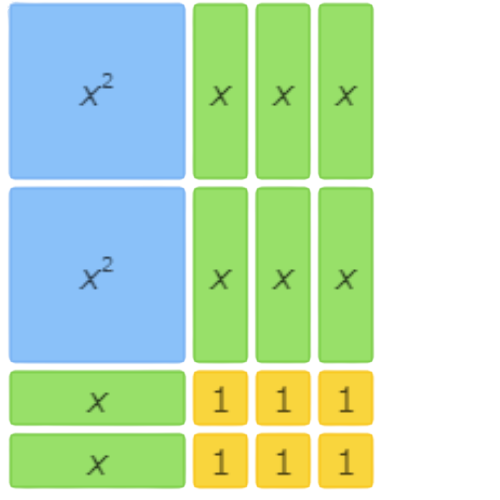
This area model shows 2x2+7x+3=(x+3)(2x+1).
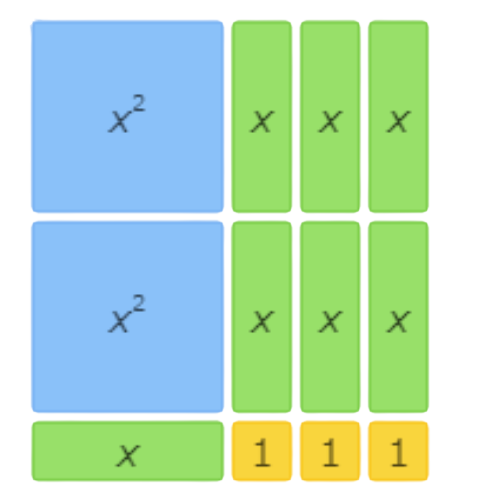
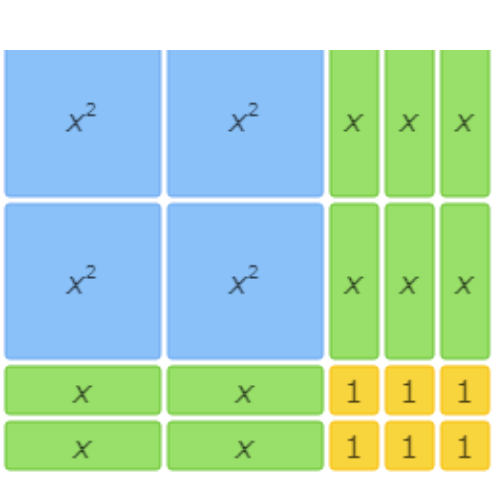
This area model shows 4x2+10x+6=(2x+3)(2x+2).
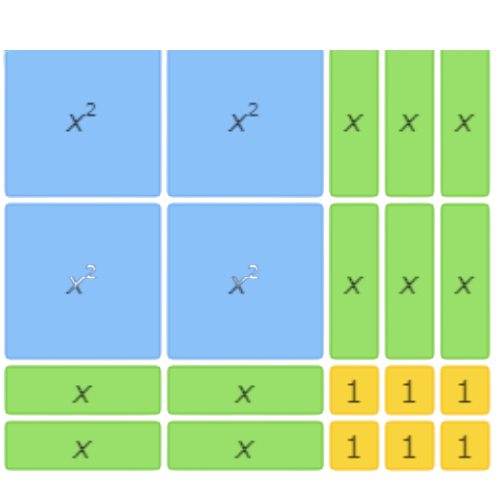
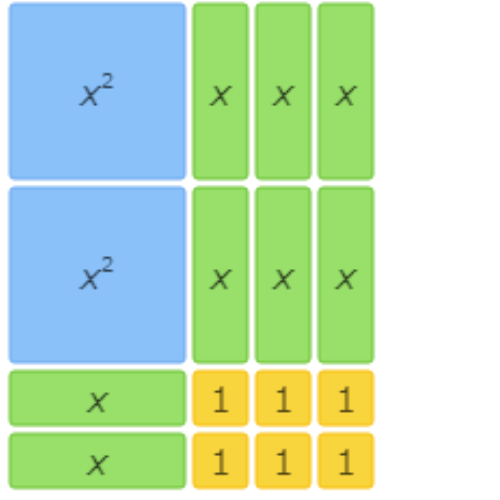
This area model shows 2x2+8x+6=(x+3)(2x+2).
🥎Which area model represents the factorisation 6x2+9x+3=(2x+1)(3x+3)?
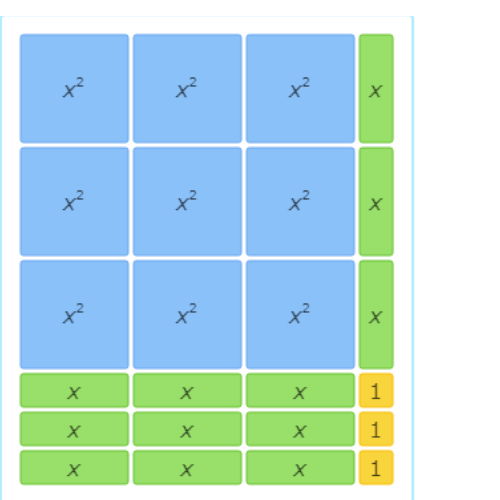
This area model represents the factorisation 6x2+9x+3=(2x+1)(3x+3).
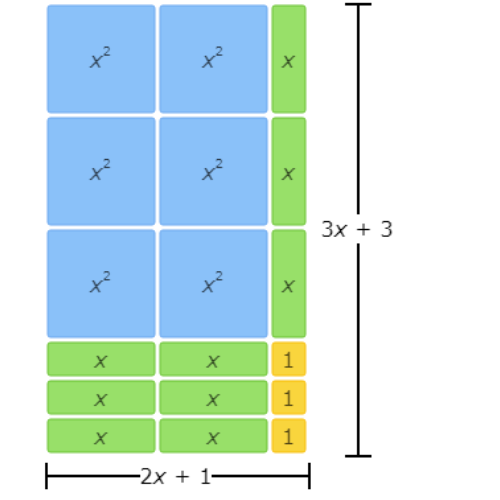
The left side of the equation represents the total area written as the sum of all the tiles. There are 6 x2 tiles, 9 x tiles, and 3 1 tiles, so the sum is 6x2+9x+3.
The right side of the equation represents the total area written as base times height. The base is made up of 2 x tiles and 1 1 tile, so it is (2x+1). The height is made up of 3 x tiles and 3 1 tiles, so it is (3x+3). The base times the height is (2x+1)(3x+3).
The other area models represent factorisations of different polynomials.
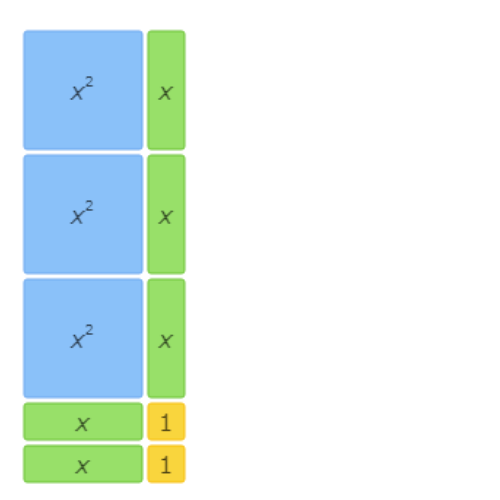
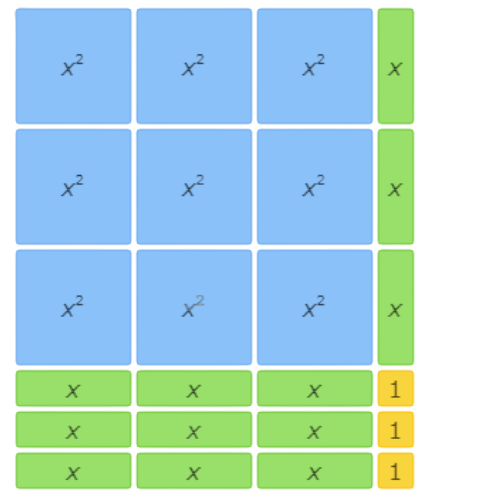
This area model shows 9x2+12x+3=(3x+1)(3x+3).
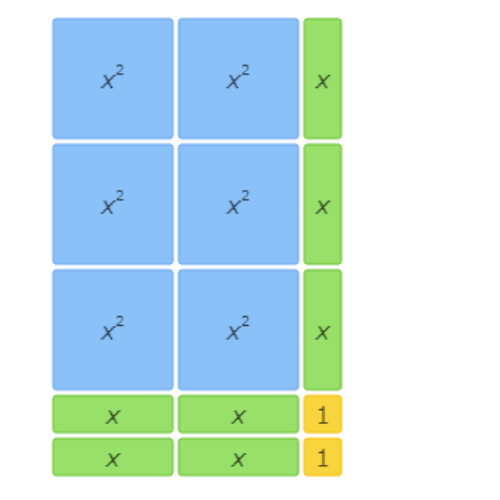
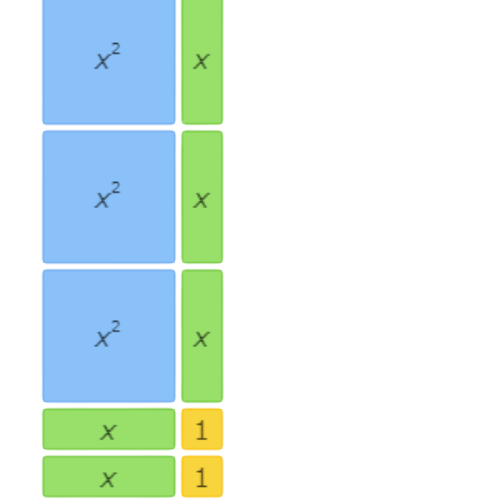
This area model shows 3x2+5x+2=(x+1)(3x+2).
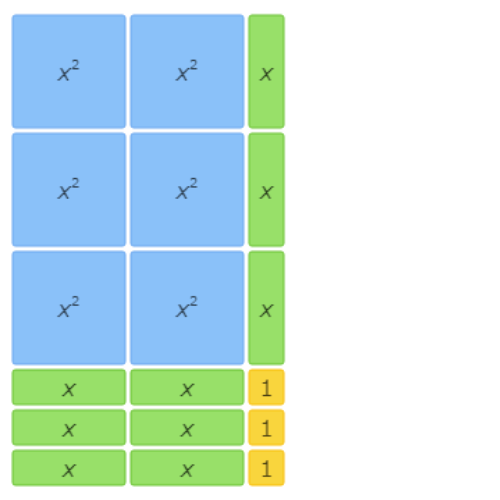
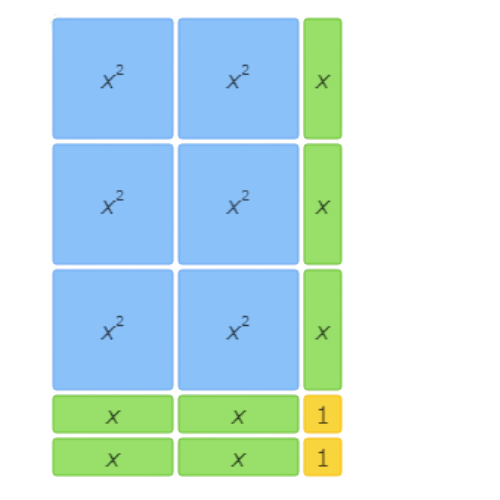
This area model shows 6x2+7x+2=(2x+1)(3x+2).
let’s practice!

