Properties of equality
Key Notes:
| What Are the Properties of Equality? |
The properties of equality are rules that help us keep an equation balanced while solving it.
They tell us what operations we can perform on both sides of an equation without changing its truth.
| Why Are They Important? |
- They help us solve equations step-by-step.
- They prevent mistakes when moving numbers or variables around.
- They keep the balance of the equation (like a scale).
| Main Properties of Equality |
1. Reflexive Property
a=a
Anything is equal to itself.
Example: 7=7
2. Symmetric Property
If a=b, then b=a.
Example: If x=5, then 5=x.
3. Transitive Property
If a=b and b=c, then a=c.
Example: If x=4 and 4=y, then x=y.
4. Addition Property of Equality
If a=b, then a + c = b + c.
(You can add the same number to both sides without changing the equation.)
Example: x=3 → x+5=3+5
5. Subtraction Property of Equality
If a=b, then a−c=b−c.
(You can subtract the same number from both sides.)
Example: x=10 → x−2=10−2
6. Multiplication Property of Equality
If a=b, then a×c=b×c.
(You can multiply both sides by the same number.)
Example: x/4=3→ Multiply both sides by 4 → x=12.
7. Division Property of Equality
If a=b, then a/c=b/c, where c≠0.
(You can divide both sides by the same non-zero number.)
Example: 5x=20 → Divide by 5 → x=4.
8. Substitution Property
If a=b, then you can replace aaa with bbb in any expression.
Example: If y=8 and 2y+1, replace y with 8 → 2(8)+1=17.
| How to Use Them in Solving Equations |
Example: Solve x−5=12
- Use Addition Property: Add 5 to both sides → x−5+5=12+5
| Quick Table |
| Property | Rule | Example |
|---|---|---|
| Reflexive | a=a | 7=7 |
| Symmetric | a=b⇒b=a | x=5⇒5=x |
| Transitive | a=b,b=c⇒a=c | 3+1=4,4=y⇒3+1=y |
| Addition | a=b⇒a+c=b+c | 4=4⇒4+2=4+2 |
| Subtraction | a=b⇒a−c=b−c | 8=8⇒8−3=8−3 |
| Multiplication | a=b⇒ac=bc | 2=2⇒2×3=2×3 |
| Division | a=b⇒a/c=b/c | 10=10⇒10÷5=10÷5 |
| Substitution | Replace equals with equals | y=6,x=y+2⇒x=8 |
| Practice Problems |
- If a=b, what is true about a+7 and b+7?
- If x−4=10, which property do you use to solve for x?
- If 3y=15, which property lets you divide both sides by 3?
- If m=2 and 2m=p2, what is p?
- If x=12, what is 5x5x5x using substitution?
Learn with an example
Which property of equality is shown below?

Find what changed.
if: t=u-28
then: t+v=c-28+v
The second equation has v added to both sides. This shows the Addition Property of Equality.
Which property of equality is shown below?

Find what changed.
if: g=-49f
then: h+g=h+-49f
The second equation has h added to both sides. This shows the Addition Property of Equality.
Which property of equality is shown below?
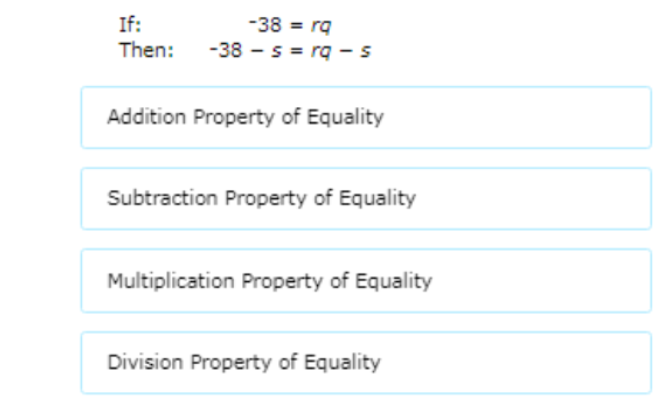
Find what changed.
if: -38=rq
then: -38-s=rq-s
The second equation has s subtracted from both sides. This shows the Subtraction Property of Equality.
let’s practice!

