Solve equations: complete the solution
| What Does “Complete the Solution” Mean? |
Sometimes an equation is partially solved or has missing steps.
“Complete the solution” means:
- Continue solving from where it is left off.
- Write all steps clearly until you find the value of the variable.
- Check the solution by substituting back into the original equation.
| Key Steps |
- Identify the current step given in the question.
- Use inverse operations to isolate the variable.
- Perform operations on both sides (maintain the balance).
- Simplify each step.
- Write the final answer for the variable.
- Verify by substituting into the original equation.
| Example Problems |
Example 1
Equation: 3x+4=13
Given Step: 3x=9
Complete the Solution:
- Divide both sides by 3:
x=9/3 - Simplify:
x=3
✅ Final Answer: x=3
🔍 Check: 3(3)+4=13 ✔
Example 2
Equation: 5x−7=18
Given Step: 5x=25
Complete the Solution:
- Divide both sides by 5:
x=25/5 - Simplify:
x=5
✅ Final Answer: x=5
🔍 Check: 5(5)−7=18 ✔
Example 3
Equation: 2(x+4)=20
Given Step: x+4=10
Complete the Solution:
- Subtract 4 from both sides:
x=6
✅ Final Answer: x=6
🔍 Check: 2(6+4)=20✔
| Common Mistakes to Avoid |
- Forgetting to do the same operation on both sides.
- Stopping before reaching the variable alone.
- Not checking the answer in the original equation.
- Ignoring negative signs.
| Practice Problems |
Complete the solutions for the following equations:
- 4x+5=21
Given Step: 4x=16 - 7x−9=26
Given Step: 7x=35 - 3(x−2)=15
Given Step: x−2=5 - 9x+12=30
Given Step: 9x=18 - 6x−4=14
Given Step: 6x=18
Learn with an example
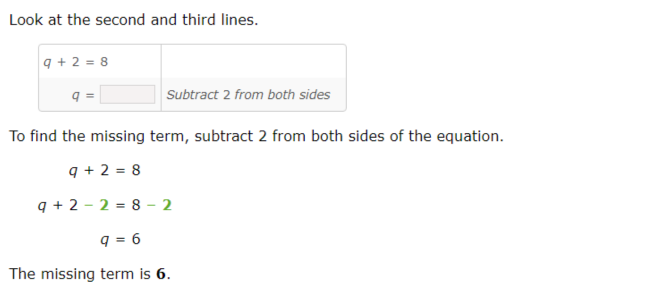
Complete the process of solving the equation.
Fill in the missing term on each line. Simplify any fractions.
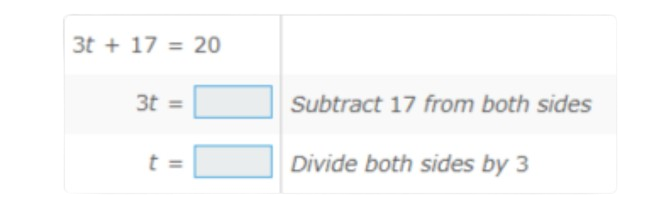
solution:
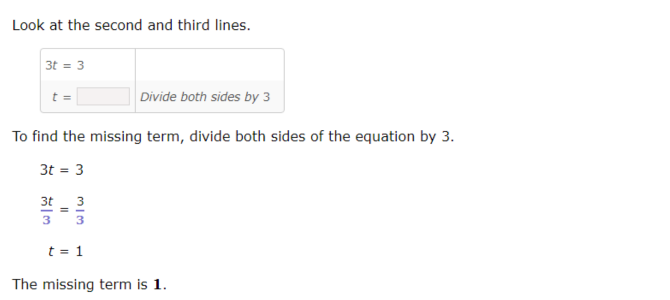
To complete the process of solving the equation, understand what changes from one line to the next.
Start at the top with the first and second lines.

Complete the process of solving the equation.
Fill in the missing term on each line. Simplify any fractions.
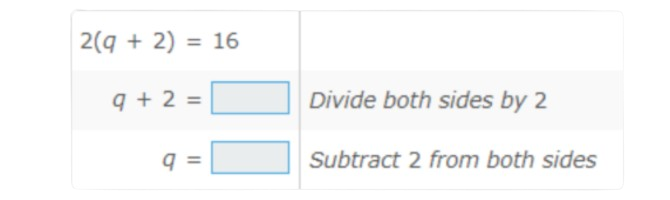
solution:
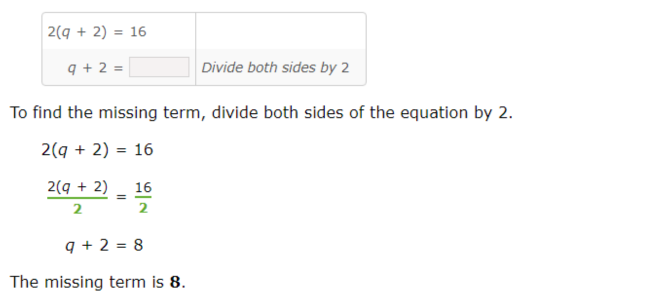
To complete the process of solving the equation, understand what changes from one line to the next.
Start at the top with the first and second lines.
let’s practice!

