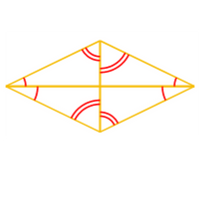
Properties of rhombuses
Key Notes:
Each diagonal of a rhombus bisects a pair of congruent opposite angles. Also, consecutive angles in a rhombus are supplementary.
Learn with an example
Quadrilateral STUV is a rhombus. What is ∠SUV?
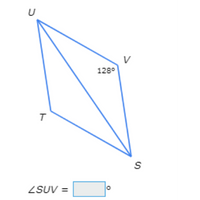
Since STUV is a rhombus, ∠TUV and ∠SVU are supplementary.
Set the sum of their measures equal to 180° and plug in ∠SVU to solve for ∠TUV.
∠SVU+∠TUV=180°
128°+∠TUV=180° Plug in ∠SVU=128°
∠TUV=52° Subtract 128° from both sides
Also, SU bisects ∠TUV, so ∠SUV=∠SUT=12∠TUV. Next, plug in ∠TUV=52° to this equation and solve for ∠SUV.
∠SUV=12∠TUV
=12(52°) Plug in ∠TUV=52°
=26° Multiply
So, ∠SUV=26°.
Quadrilateral GHIJ is a rhombus. What is ∠FIH?
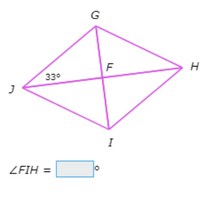
Since GHIJ is a rhombus, opposite angles are congruent, GI bisects ∠HIJ, and HJ bisects ∠GJI.
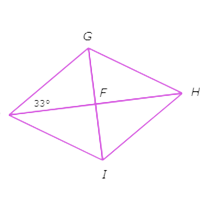
So, ∠FJG≅∠FJI≅∠FHG≅∠FHI and ∠FGH≅∠FGJ≅∠FIH≅∠FIJ. Specifically ∠FHI=∠FJG=33°. Also, since GI and HJ are perpendicular, ∠HFI=90° and △FHI is a right triangle.
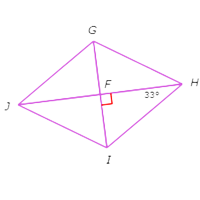
This means ∠FHI and ∠FIH are complementary. Set the sum of their measures equal to 90° and plug in ∠FHI=33° to solve for ∠FIH.
∠FHI+∠FIH=90°
33°+∠FIH=90° Plug in ∠FHI=33°
∠FIH=57° Subtract 33° from both sides
So, ∠FIH=57°.
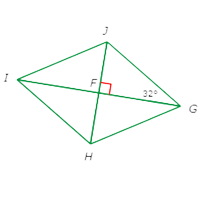
Quadrilateral GHIJ is a rhombus. What is ∠FJG?
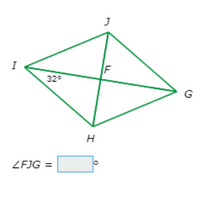
Since GHIJ is a rhombus, opposite angles are congruent, GI bisects ∠HIJ, and HJ bisects ∠GJI
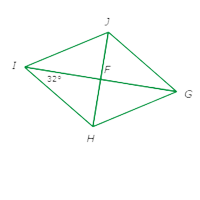
So, ∠FIH≅∠FIJ≅∠FGH≅∠FGJ and ∠FHG≅∠FHI≅∠FJG≅∠FJI. Specifically ∠FGJ=∠FIH=32°. Also, since GI and HJ are perpendicular, ∠GFJ=90° and △FGJ is a right triangle.
let’s practice!

