do the ratios form a proportion: word problems
Key Notes :
👉 A proportion is a statement that two ratios are equivalent to each other. Two ratios form a proportion if their cross-products are equal.
Learn with an example
✈️ Do these ratios form a proportion?
30 large blankets: 35 medium blankets
6 large blankets: 7 medium blankets
- yes
- no
Write the ratios as fractions.
30/35 and 6/7
Compare the two fractions to see if they are equivalent.
30 × 7 = 35 × 6 ——-> Multiply both sides by 35 × 7
210 = 210 ——-> Simplify
The cross-products are equal, so the ratios form a proportion.
✈️ Do these ratios form a proportion?
9 large cars: 2 medium cars
19 large cars: 7 medium cars
- yes
- no
Write the ratios as fractions.
9/2 and 19/7
Compare the two fractions to see if they are equivalent.
9 × 7 = 2 × 19 ——> Multiply both sides by 2 × 7
63 ≠ 38 ——> Simplify
The cross-products are not equal, so the ratios do not form a proportion.
✈️ Do these ratios form a proportion?
5 items every 40 days
3 items every 31 days
- yes
- no
Write the ratios as fractions.
5/40 and 3/31
Compare the two fractions to see if they are equivalent.
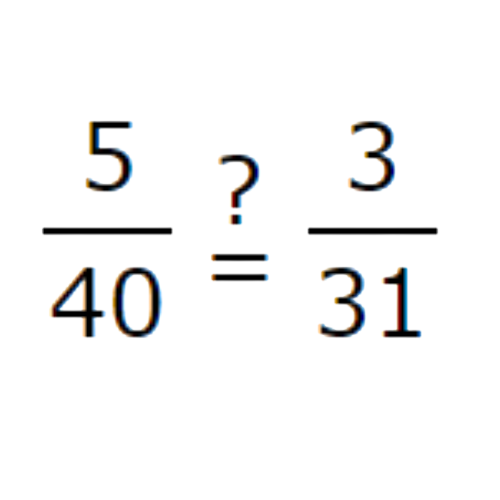
5 × 31 = 40 × 3 ——-> Multiply both sides by 40 × 31
155 ≠ 120 ——> Simplify
The cross-products are not equal, so the ratios do not form a proportion.
Let’s practice! 🖊️
