Evaluate negative exponents

Key Notes :

1. Definition of Negative Exponent

  • A negative exponent represents the reciprocal of the base raised to the positive exponent.

2. Understanding Negative Exponents

  • If an exponent is negative, the base is placed in the denominator as a positive exponent.

3. Rules for Negative Exponents

  • This means to evaluate a negative exponent, take the reciprocal of the base and change the sign of the exponent.
  • Multiply the bases and add the exponents when they are negative.
  • Divide the bases and subtract the exponents when they are negative.

4. Examples of Negative Exponents

5. Simplifying Expressions with Negative Exponents

  • When simplifying expressions, apply the negative exponent rule to convert negative exponents to positive ones.

6. Important Notes

Learn with an example

Write the expression as a fraction with a positive exponent. Do not evaluate the expression.

9-2

The base has a negative exponent, –2. You can rewrite the expression as a fraction with a numerator of 1 and a positive exponent, 2, in the denominator.

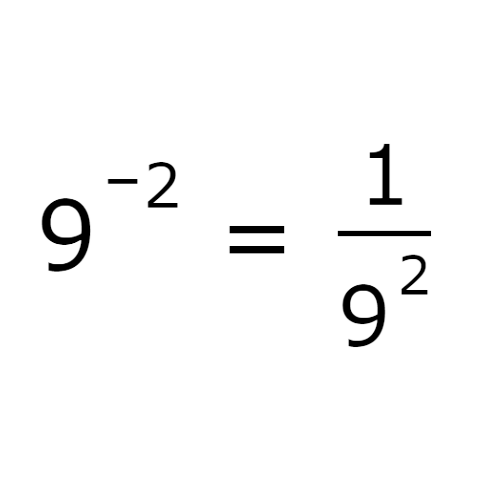
Write the expression as a whole number with a negative exponent. Do not evaluate the expression.

1/73

There is a positive exponent, 3, in the denominator. You can rewrite the expression with an exponent of –3 instead.

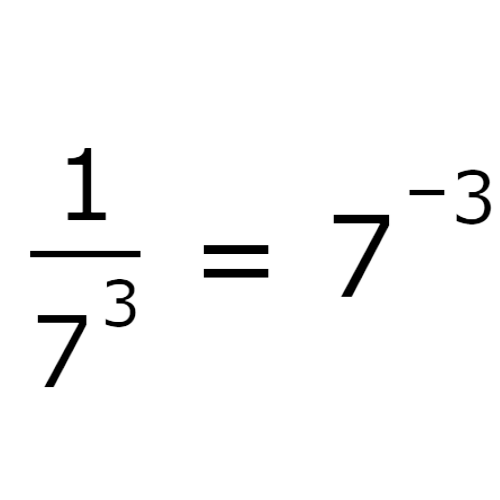
Evaluate. Write your answer as a fraction or whole number without exponents.

3–3 =

Let’s practice!🖊️