Changes in mean, median, mode and range

key notes :

Mean:

Formula:

The mean is the average of a set of numbers.

To find the mean, add all the numbers together and divide by the total count of numbers.

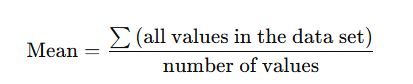
Changes in Mean:

• If you add or remove a number, the mean will change based on the value of the number.
• A large value added or removed will cause a bigger shift in the mean compared to a smaller value.

---

Median:

The median is the middle value when the data is arranged in ascending or descending order.

If there’s an odd number of values, the median is the middle number.

If there’s an even number of values, the median is the average of the two middle numbers.

Changes in Median:

• Adding or removing numbers can change the position of the median.
• If the data set is large, changes in individual values might not affect the median unless the new values push the middle numbers.

---

Mode:

The mode is the number that appears most frequently in a data set.

• A data set can have:
• One mode (unimodal).
• Two modes (bimodal).
• More than two modes (multimodal).
• No mode if no number repeats.

Changes in Mode:

• If a new number is added that already exists in the data set, the mode might remain the same or change.
• If a new number is added that is different from all the others, the mode might stay the same, or there might be no mode.

---

Range:

• The range is the difference between the highest and lowest values in the data set.
• Formula:

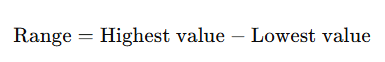
Changes in Range:

• Adding a number greater than the current highest value increases the range.
• Adding a number smaller than the current lowest value also increases the range.
• Removing the highest or lowest value can decrease the range.

---

General Impact of Changes:

Addition/Removal of Numbers:

• Adding numbers can shift the mean, median, and range depending on the values added.
• Removing numbers can also affect all measures, especially if the number removed is the highest, lowest, or middle value.

Effect of Extreme Values (Outliers):

• Outliers (extremely high or low values) can significantly affect the mean and range but have less effect on the median and mode.

Learn with an example

let’s practice!